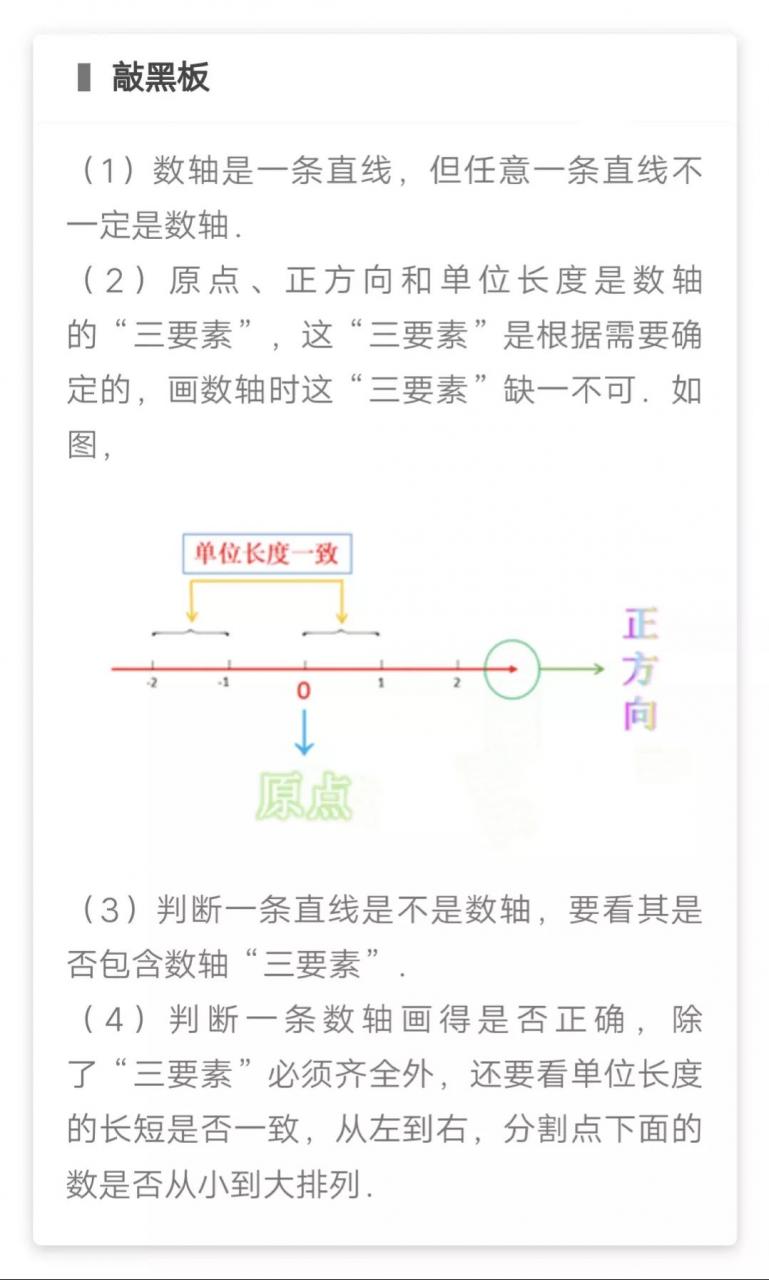
数轴:规定了原点、正方向和单位长度的直线叫做数轴(画数轴时,要注意上述规定的三要素缺一不可)。
解题时要真正掌握数形结合的思想,理解实数与数轴的点是一一对应的,并能灵活运用。
①画一条水平直线,在直线上取一点表示0(原点),选取某一长度作为单位长度,规定直线上向右的方向为正方向,就得到数轴(“三要素”)
②任何一个有理数都可以用数轴上的一个点来表示。
③如果两个数只有符号不同,那么我们称其中一个数为另外一个数的相反数,也称这两个数互为相反数。
作用:A.直观地比较实数的大小;B.明确体现绝对值意义;C.建立点与实数的一一对应关系。
数轴:规定了原点.正方向和单位长度的直线.
注意:
⑴原点.正方向.单位长度称为数轴的三要素,三者缺一不可.
⑵单位长度和长度单位是两个不同的概念,前者指所取度量单位的长度,后者指所取度量单位的名称,即单位长度是一条人为规定的代表“1’的线段,这条线段可长可短,按实际情况来规定,同一数轴上的单位长度一旦确定,则不能再改变.
⑶数轴的画法及常见错误分析
①画一条水平的直线;
②在这条直线上适当位置取一实心点作为原点:
③一般确定向右的方向为正方向,用箭头表示;
④选取适当的长度作单位长度,用细短线画出,并对应标注各数,同时要注意同一数轴的单位长度要一致.
2.数轴画法的常见错误举例:
3.有理数与数轴的关系:
1.一切有理数都可以用数轴上的点表示出来.
2.在数轴上,右边的点所对应的数总比左边的点所对应的数大.
3.正数都大于0,负数都小于0,正数大于一切负数.
注意:数轴上的点不都代表有理数,如 π.
4.利用数轴比较有理数的大小:
数轴上右边的数总大于左边的数.因此,正数总大于零,负数总小于零,正数大于负数。
(2)所有的有理数都能用数轴上的______来表示。
(3)数轴上,表示-3的点到原点的距离是______个单位长,与原点距离为3个单位长的点表示的数是______。
(4)数轴上A,B两点分别在原点的两旁,并且与原点的距离相等,已知点A表示的数是-10,则点B表示的数为______。
(5)如图,有理数a,b在数轴上对应的点如下,则有( )。
答案:
(1)原点;正方向;单位长度;直线.(按照定义做)
(2)点。
(3)3;+3和-3.(距离为正;原点两侧到原点的距离相等的点所对应的数各有一个,
所以有两个数,即为+3和-3。)
(4)10/+10.(同上)
(5)C.(数轴上,右边的点所对应的数总比左边的点所对应的数大。


测 试 题
例1.如图所示是几位同学所画的数轴,其中正确的是( )
A.(1)(2)(3) B.(2)(3)(4) C.只有(2) D.(1)(2)(3)(4)
【答案】C
【解析】对数轴的三要素掌握不清.(1)中忽略了单位长度,相邻两整点之间的距离不一致;(3)中负有理数的标记有错误;(4)图中漏画了表示方向的箭头.
【总结升华】数轴是一条直线,可以向两端无限延伸;数轴的三要素:原点、正方向、单位长度缺一不可.






数轴:规定了原点、正方向和单位长度的直线叫做数轴
数轴的三要素:原点、正方向和单位长度(画数轴时,三要素缺一不可)。要点:任何一个有理数都可以用数轴上的一个点来表示(有理数的数轴表示,体现了数形结合的数学思想)。
导学案
2.2数轴
一、学习目标
1.掌握数轴的三要素,会画数轴
2.能将已知数在数轴上表示出来,能说出数轴上已知点所表示的数
3.经历数轴形成的过程,初步体会数形结合的思想方法
二、重点:数轴的画法;会用数轴上的点表示有理数,能说出数轴上已知点所表示的数.
三、难点:会用数轴上的点表示有理数,能说出数轴上已知点所表示的数
四、自学指导(10分钟)
首先请同学们阅读下课本7-9页的内容,然后回答下列问题:
(一)数轴的概念
1、在直线上任取一个点表示数0,这个点叫做
2、通常规定直线上从原点向右(或向上)为,从原点向为负方向
3、选取适当的长度作为,从直线上原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法表示-1,-2,-3,…;那么根据以上的问题,我们就可以得出以下的结论:规定了、和的直线叫做数轴.
(二)数轴的画法.
1、画一条数轴:
2、下面的数轴画地对不对?如果不对,请指出错在哪里
3、指出数轴上的点A、B、C、D分别表示什么数..指出在数轴上表示下列各数的点分别位于原点的哪边,与原点距离多少个单位长度.
五、当堂练习
1、判断题
(1)直线就是数轴()
(2)数轴是直线()
(3)任何一个有理数都可以用数轴上的点来表示()
(4)数轴上到原点距离等于3的点所表示的数是+3()
数轴上原点左边表示的数是负数,右边表示的数是正数,原点表示的数是0.()

 大象juǎn
大象juǎn